ФРАКТАЛЬНАЯ ГЕОМЕТРИЯ В ПРИЛОЖЕНИИ К ФРАКТАЛЬНОЙ ФИЗИКЕ
Шабетник Василий Дмитриевич.
Российская академия космонавтики
IX Международная конференция математика, образование, экономика, экология г. Чебоксары, 28 мая – 2 июня 2001 г.
Окружающий нас мир состоит из фрактальных форм, которые с недавних пор оказались в центре внимания учёных. Ведь в последние годы Б.Мандельбротом [1] и другими авторами [2-8] для описания разветвлённых объектов разработана фрактальная геометрия. Б.Мандельброт ввёл термин «фрактал» и общее понятие фракталов. Название «фрактал» происходит от латинского fractus, что означает дробный, ломаный. Поэтому понятие фрактала связывают с шероховатой поверхностью рассматриваемых физических объектов или с изломанными формами их атомной структуры, обладающими свойством самоподобия. В основе этого свойства фракталов содержится одна важная особенность: фрактальные объекты самоподобны, т.е. их вид не меняется в любом пространственном масштабе. Хотя эта особенность является упрощением действительности, она значительно увеличивает глубину нашего описания природы. Можно сказать, что идея фракталов была выдвинута вовремя: само понимание мира шло навстречу фракталам, ибо мир по своей структуре (форме) является фрактальным, а по сущности (содержанию) - электрическим.
Однако фрактальная геометрия как математическая наука имеет ограничения на исследование объектов и изучает формы в таких разветвлённых системах, как береговые линии, горные цепи, турбулентность, формы облаков, молний, деревьев и т.д. Основой фрактальной геометрии является аффинная геометрия. Понятие аффинного пространства предполагает, что это пространство лишено метрики, т.е. способа измерения длин и углов. В нём определён только конкретный вид правил образования суммы элементов и произведения элемента на число. При этом элементы аффинного пространства принято в узком смысле называть векторами, а само пространство -точечно-векторным, ибо ввели в рассмотрение ещё и точки. Ведь точка - основное понятие в геометрии, которую изучают в средней школе, а все её геометрические образы можно понимать как множества точек; в то же время в определении векторного пространства точки вообще не фигурируют. Поэтому такое множество векторов и точек аффинного пространства ближе к тому пространству, которое изучается в курсе элементарной геометрии, хотя и не будет еще полностью совпадать. Аффинное пространство станет вполне идентичным (во всяком случае для двух- и трёхмерного случаев) обычному пространству лишь после введения в нём соответствующей метрики. В обычном трёхмерном пространстве метрика вводится как произведение длин векторов, умноженное на косинус угла между ними. Тогда такое векторное пространство с введённой метрикой называется евклидовым пространством.
Отсюда видим главное отличие фрактальной геометрии, что она не занимается изучением обычных объёмных тел и, конечно, изменением их объёма; аффинная геометрия также не занимается природой фрактальных форм. Мы воспользуемся только её названием и будем в дальнейшем усовершенствовать математический аппарат в качестве инструмента для изучения физических явлений. Здесь ради истины следует сказать, что физическое начало изучения формообразования природных объектов положил И.Кеплер (1571 - 1630) [9]. Однако пионером фрактальной геометрии следует считать Секста Эмпирика (II в. после Р.Х.) [10], ибо он первым обратил внимание на ширину линии, на ограниченность представления о размерности как непременно о целом числе. Теперь мы более сведущи и более подготовлены, поэтому перед нами открываются большие возможности фрактального анализа. Сущность фрактального анализа заключается в том, что в нём рассматриваются совокупности точек в качестве основных объектов. Эта особенность аффинной геометрии согласуется с фундаментальной структурой фрактальной физики, в которой частицы, электроны, ядра представляются электрическими зарядами, а, например, Галактика как совокупность заряженных звёзд типа Солнца. Положение существенно изменилось после того, как была установлена новой наукой о мироздании [11] связь фрактальных структур и их размерностей с энергетическими характеристиками системы. В последнее время были найдены формы описания всех эффектов взаимодействий объектов единой, электромагнитной природы, для которых пространство основных состояний описывается в терминах фракталов. При развитии теории фракталов введено фрактальное дифференцирование (интегрирование), так как фрактальная геометрия [2, 7, 8] отказывает в дифференцируемое™ некоторых фрактальных движений, ибо использует классическое приближённое вычисление, и определены фрактальные размерности физических объектов и их связь с энергетическими характеристиками систем, а также обнаружены новые, неизвестные ранее закономерности [12].
Действительно, фрактальная физика [12, 13] - это наука о мире в целом - обнаружила и установила, что все явления и процессы имеют единое фундаментальное взаимодействие, электромагнитное по своей сущности, и проявляются они в форме различных фрактальных, электрических структур, которые могут быть и не самоподобны. Поэтому пространство взаимодействий физических объектов описывается как евклидовой, так и аффинной геометриями. Такое различие связано с тем, что при анализе процессов микромира значения приращений пространства не следует, в отличие от евклидовой геометрии, выбирать произвольно. Знаем [12, 13], что микроструктура пространства образуется комбинациями элементарных электрических зарядов. Вот почему новая наука описывает адекватно реальности взаимодействие частиц микромира в аффинном пространстве, где отсутствует измерение длины и площадей. Кроме того, достигнутые фрактальной физикой результаты указывают на то, что фрактальная геометрия не знала о них и поэтому не могла изучать эти физические объекты ввиду своей ограниченности. Как это часто бывает, многие работы по фрактальной геометрии следует рассматривать скорее как конспективные заметки или краткие тезисы по вопросу определения фрактальной размерности разветвлённых объектов, ибо в них не просматривается глубокой связи с энергетическими показателями взаимодействующих систем. Прилагаемый список литературы даёт возможность достаточно быстро войти в рассматриваемую проблему. Для читателей, желающих ознакомиться с первоначальными понятиями и современной точкой зрения на теорию фракталов, имеются хорошие обзоры [4, 14].
Новая физика использовала введённое геометрией понятие фрактальной размерности D и расширила её применение для различных материальных объектов. Фрактальная размерность выступает в качестве количественной меры структурности этих объектов. Для определения D вспомним понятия обычной евклидовой геометрии. Рассмотрим сплошной круговой или сферический объект массой М и радиусом R . Если объект круговой или сферический, то при увеличении радиуса объекта его масса увеличивается в R2или в R3. Эту связь массы и длины можем записать в виде М ~ RE , где Е -размерность (число координат) пространства. Объект называется "фрактальным", если он удовлетворяет соотношению М ~ RD , где D меньше пространственной размерности Е. Это указывает на то, что фрактальная геометрия описывает объекты с дробной размерностью пространства.
Однако в реальных физических системах фрактальная размерность D выполняется не для любых масштабов длины, а ограничивается верхними и нижними пределами фрактальных объектов, которые являются не самоподобными. Поэтому вводятся два совершенно различных значения размерности: локальное (справедливое для масштабов, меньших некоторого критического) и глобальное (справедливое для масштабов, больших критического). Эти размерности принципиально отличаются, поэтому в разных физических задачах нужно пользоваться разными определениями фрактальной размерности.
Например, глобальная размерность (иногда называют внешняя размерность) кривой фрактального типа на плоскости изменяется от 1 до 2, где 1 - размерность прямой, 2 - размерность плоскости. Локальная (иногда называют внутренняя размерность) для этой кривой на плоскости изменяется от 1 до бесконечности. Эти размерности -глобальная и локальная - совпадают только для тривиального случая гладкой кривой. Тогда становится понятным, что глобальная размерность фрактальной кривой изменяется от размерности гладкого объекта до размерности пространства, а локальная - от размерности гладкого объекта до бесконечности. Теперь обсудим фрактальную размерность на примере регулярных, самоподобных фракталов. Рассмотрим сначала отрезок единичной длины, который разбит на N равных кусков длиной b, так что N = 1/b. По мере уменьшения b значение N растёт линейно, что и следовало ожидать для одномерной кривой. Аналогично, если мы разделим квадрат единичной площади на N равных квадратиков со стороной b, то получим N = 1/b2 - ожидаемый для двумерного объекта результат. Можно утверждать, что в общем случае N = 1/bD, где D размерность объекта. Следовательно, логарифмируя обе части этого равенства, можно выразить размерность в виде
D=logN/log(1/b), (1)
которая не зависит от основания логарифма.
Теперь применим эти соображения к так называемой кривой Коха (см. п.1 табл. 1). На рисунке этого пункта кривая Коха представлена после трёх стадий своего формирования. На каждой стадии формирования этой кривой замена средней трети каждого сегмента производится в направлении, которое увеличивает площадь под кривой. Можно увидеть, что при каждом уменьшении длины b в три раза число сегментов увеличивается в четыре раза. Таким образом имеем N = 4 и b = 1/3, и фрактальная размерность треугольной кривой Коха равна D = ln4/lnЗ = 1,2618... Это выражение является инвариантом, то есть остаётся неизменным для любого числа k-звеньев (сегментов) кривой, ибо
D=ln4k/ln3k=1,2618... (2)
Здесь для удобства определения размерности использован натуральный логарифм.
Можно сделать заключение, что глобальная фрактальная размерность оценивает рост числа множеств (объектов) бесконечно малого диаметра, необходимых для того, чтобы покрыть данное множество (форму). Вообще существуют различные видоизменения понятия [4] фрактальной размерности - насчитывается 12 способов её описания. Однако большинство авторов называют множество фрактальным, если его размерность Хаусдорфа не является целым числом и оценивает рост объектов бесконечно малого диаметра в соответствии с вышеуказанным определением. В работе дана единая формулировка DG глобальной фрактальной размерности в смысле Хаусдорфа.
Для понимания определения глобальных размерностей DG приведем конструкции производящих фрактальных форм, приставленных в таблице 1.
Таблица1. конструкции производящих фрактальных форм
1)Кривая Коха(треугольная)
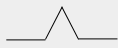
|
DG =log4/log3 = 1.2618...
N=4, b=1/3
|
2) Видоизменённая кривая Коха
(прямоугольная)

|
Единичный сегмент имеет три отрезка длиной 1/3. два отрезка длиной 1/4. Из соотношения 3(1/3)D + 2(1/4)D = 1
DG= 1.34.
|
3)>Видоизменённая
кривая Коха (меандр)
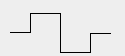
|
DG =log8/log4 = 3/2
N=8, b=1/4
|
4)Канторовская пыль
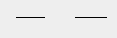
|
DG =log2/log3 = 0,6309...
N=2, b=1/3
|
5)Дерево
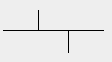
|
DG =log5/log3 = 1,465...
N=5, b=1/3
|
6) Снежинка

|
DG =log3/log(3)1/2 = 2
N=3, b=1/(3)1/2
|
7) Прокладка Серпинского

|
DG =log3/log2 = 1,585...
N=3, b=1/2
|
В таблице 1 производящих форм
в п.6
представлена треугольная снежинка. Формообразование шестиугольной снежинки Кеплера
[9] строится продолжением трёх лучей исходной треугольной снежинки. Следует обратить
внимание, что при этом все пушинки этой снежинки от центра направлены наружу, как
иголки на еловой ветке. Это свидетельствует о том, что формообразующая сила сосредоточена
в центре снежинки и действует оттуда одинаково по всем направлениям. Можно сказать,
что снежинка неотделима от формообразующего начала, называемого электрическим зарядом.
Действительно, фрактальная размерность снежинки Кеплера
характеризует количество информации, которое в среднем может
переносить одна медленная электрическая частица с полуцелым
спином. Для понимания можно воспользоваться результатами работы [15], в соответствии
с которыми среднее количество информации на одну частицу принимает следующие значения:
для быстрых и медленных бозонов соответственно 3,60 и 2,19, а для быстрых и медленных
фермионов количество информации соответственно 4,2 и 3,28. Следует напомнить, что
частицы с целым спином называют бозонами. К ним относится и фотон. К фермионам относятся
частицы с полуцелым (дробным) спином, например, субатомные
частицы. Известно [12], заряд снежинки является порождением электрической силы Земли.
Отсюда следует, что в любом веществе, в любом растении формообразующее начало определяется
электрическим зарядом и в зависимости от внутренних свойств веществ строит ту или иную внешнюю форму.
В то же время понятие локальной фрактальной размерности DLсвязывают с понятием меры множества
в соответствии с известным из элементарной геометрии понятием объёма [16]. Вообще
мера протяжённости и искривлённости множества также называется мерой Хаусдорфа. Локальная фрактальная размерность DLхарактеризует объём этого множества
(объекта) с учётом протяжённости соприкосновения общих элементов его форм. Понятие
"объём" следует понимать как "квазиобъём",
ибо отличие состоит в том, что в случае объёма всякая точка, отрезок или лист имеют
меру (объём) 0, а в случае квазиобъёма это может быть
и не так. Кроме того, схема наших построений может быть распространена на некоторые
квазиобъёмы, которые принимают и отрицательные значения.
Иногда вместо понятия "квазиобъём" применяют
термин "мощность", который также является аналогом понятия локальной размерности.
Для понимания определения размерностей в таблице 2 приведены
фрактальные размерности физических объектов. В связи с ограничением объёма данной
статьи дальнейшее обоснование теории фракталов: фрактальное дифференцирование (интегрирование),
фрактальные размерности физических объектов, связь фрактальных форм и их размерностей
с энергетическими характеристиками систем -не приводится,
однако описание структур и изложение решения данной проблемы,
как создание фрактальной (природной) математики
, можно найти в [11,
12, 17].
Таблица 2. Фрактальные размерности физических объектов
1) Проекция формы электрона
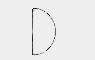
|
s= 1/2
|
2)Проекция
формы фотона
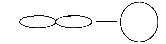
|
s=1
|
3) Взаимодействие
двух электронов
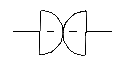
|
DL = 10,00049
DG = ln2/lnЗ = 0.6309...
|
4)Протон
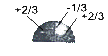
|
DL = 12,0944
s=1/2
|
5) Нейтрон

|
DL = 9,2146
s=1/2
|
6) Модель
атома водорода
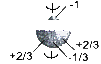
|
WH= 4πq + 1 = 13,6 эВ
Wатом = 13,6Z2
|
7)Структура
пространства
1.
Вихревая структура
пространства
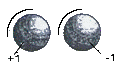
|
DL = 8
π
DG = 0,962 ≈ 1
|
2.Квазикристаллическая структура
пространства

|
DL→ ∞
DG = 1
|
8) Фрактальная размерность заряженной
материальной точки

|
D=m/q =4π
(система СИ)
|
9) Фрактальная размерность Солнца и
Галактики
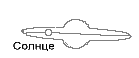
|
DL = M/Q=0,5 *1016
DG = m/q=4
π
(система СИ)
|
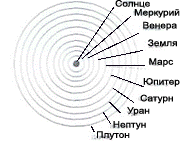
10) Связь локальной фрактальной размерности Солнечной системы
с локальной фрактальной размерностью планеты Плутон:
Σ(m/q)
планета=2(m/q)
Плутон, причем Σ(m/q)планета = 4,4-10
18, (m/q)
Плутон = E
2(M/Q)
Солнце, величина напряженности
электрического поля Е
Плутон = 21 В/м.
11)Локальные фрактальные размерности планет Солнечной системы и
Луны: для Земли (m>/q) = 0,8·10
16 , для Луны - 0,3·10
16,
для Венеры - 0,5 10
16 (по величине совпадает с размерностью Солнца и
Галактики), для Меркурия -0.2·10
16, для Марса - 1.6·10
16,
для Юпитера - 0,1·10
18, для Сатурна - 0,3·10
18,
для Урана - 0,8·10
18, для Нептуна - 1·10
13,
для Плутона - (m/q) = 2.2·10
18
12) Закон построения Солнечной системы в
геометрической и электрической формах (система СИ):
rCолнце=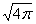 ·ΣrПланет, rЗемля= ·ΣrПланет, rЗемля=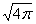 · rЛуна, · rЛуна,
причем rСолнце=7·105 км, ΣrПланет=2·105 км, rЗемля=6371 км, rЛуна=1737 км.
сСолнце=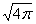 ·ΣсПланет, сЗемля= ·ΣсПланет, сЗемля=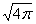 ·сЛуна, ·сЛуна,
причем сСолнце=78 600 мкФ, ΣсПланет=22 344 мкФ, сЗемля=690 мкФ, сЛуна= 194 мкФ
|
13)Фрактальная
размерность электронных оболочек атома
Размерность электронных оболочек представлена в [11, 12].
14) Фрактальная размерность ядер атомов
Размерность ядер атомов представлена в [11, 12].
Достигнутые результаты позволили представить новое учение
о мире в целом "Фрактальная физика. Наука о мироздании" [12], как единственный
пример объединения естественнонаучного и духовного направлений в современной науке
[18].
ЛИТЕРАТУРА
-
Mandelbrot B.B. The Fractal Geometry of Nature. W.H.Freeman
and Company,
1983. - 468p.
- Falconer K.J.
Fractal Geometry.Mathematical Foundations
and Applications
J.Wiley&Sons, 1995.- 288p.
-
Peitgen H.-O., Jorgens H., Saupe D.
Fractals for the Classroom. Part One:
Introduction to fractals and chaos. Part two: Complex systems and Mandelbrot
set. Springer-Verlag, 1993.- 452p. and - 500p.
-
Takayasu H. Fractals in the Physical Sciences.J.Wiley&Sons 1990. -170p.
-
Пайтген Х.-О., Рихтер П.Х. Красота фракталов.
Образы комплексных
динамических систем. М.: Мир, 1993. - 176с.
-
Фракталы в физике. Под ред. Л.Пьетронеро и Э.Тозатти. М.: Мир, 1988. -670с.
-
Федер Е. Фракталы. М.: Мир, 1991. - 262с.
- Кроновер P.M. Фракталы и хаос в динамических системах.
Основы теории. М.: Постмаркет, 2000. -352с(- С.262,
273).
- Кеплер И. О шестиугольных снежинках. М.: Наука, 1982, - 192с (-С.5-32).
- Секст Эмпирик. Сочинения в двух томах. М.: Мысль, 1976. Т. I. - С.303-315.
- Шабетник В.Д. Физическая мысль России, №2,
1996, - С.60-66.
- Шабетник В.Д. Фрактальная физика. Наука о
мироздании. М.:Тибр,2000.-416с.
- Шабетник В.Д. Фрактальная физика. Введение
в новую физику. 2-е изд. На англ. и русск. язык. Каунас, Gylys, 1994. -72с.
- Зельдович Я.Б., Соколов Д.Д. Фрактали,
подобие, промежуточная
асимптотика. "Успехи физических наук", т. 146, вып.3,1985. - С.493-506.
- Левитин Л.Б. Физические ограничения в каналах передачи информации.
ГГУ: Кандидатская диссертация, 1969. - 196л (- Л.85-87).
- Шилов Г.Е., Гуревич Б.Л. Интеграл, мера и производная.
М.:Наука, 1964.-212с.
- Шабетник В.Д., Шабетник Д.В., Шабетник П.В. Физическая мысль России,
№2, 2000.-С.91-104.
- Шабетник В.Д. Фрактальная физика как учение
о мироздании - пример
объединения естественнонаучного и духовного направлений в образовании.
"Математика. Компьютер. Образование". Вып.7, Часть 1. Сборник научных
трудов. Под ред. Г.Ю.Ризниченко. М.: Прогресс-Традиция, 2000, -С. 25, 79-88.
Сайт создан в системе
uCoz
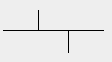


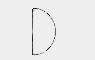
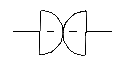
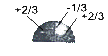

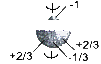



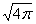 ·Σr
·Σr
